Web日本評論 > お知らせ > 出題（2025年10月号掲載分）／応募締切（10月8日）／解答（2026年1月号掲載）

出題（2025年10月号掲載分）／応募締切（10月8日）／解答（2026年1月号掲載）

エレガントな解答をもとむ(数学セミナー)｜ 2025.09.11

『数学セミナー』のコーナー「エレガントな解答をもとむ」の出題を掲載します．奮ってご応募ください．解答・講評(3ヶ月後)は，本誌にてご確認ください．

(毎月10日頃の掲載予定)

$\def\t#1{\text{#1}}\def\dfrac#1#2{\displaystyle\frac{#1}{#2}}\def\rC{\text{C}}$

出題1

縦 $4$ 行，横 $7$ 列のマス目に 1 つずつ石が置かれています．これに対して以下の操作を有限回行います：

$2\times 2$ の正方形状に並んだ $4$ マスを選び，その片方の対角線上の $2$ マスから $1$ つずつ石を取って，もう片方の対角線上の$2$マスに$1$つずつ置く．

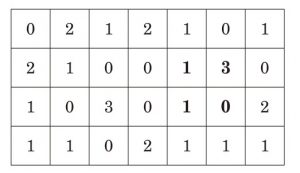
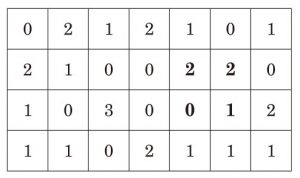
たとえば，石の個数が図 1 のようになっているとき，$1$ 回の操作で図 2 の状態にすることができます．石が $1$ つ以上置かれているマスの個数は，いくつまで減らせるでしょうか．その最小値を求め，それが最小であることを証明してください．

余力があれば，マス目の縦と横の長さが一般の場合も考えてみてください．

図1　操作前の石の個数

図2　操作後の石の個数

出題：小泉淳之介 (理化学研究所数理創造研究センター)

出題2

$a=(a_i)_{1\leqq i \leqq n}$ を正整数からなる長さ $n$ の数列とする．各整数 $a_1, a_2, \cdots, a_n$ を $n$ 個のボールに一つずつ書き込み，袋に入れ以下の操作を繰り返す．

袋からボールを $2$ 個取り出し，各ボールに書かれた整数をそれぞれ $p,\, q$ とする．
新しいボールに整数 $\lceil (p+q)/2 \rceil$ を書き込み袋に入れる．

ただし，実数 $s$ に対して $\lceil s \rceil$ は $s$ 以上の最小の整数を意味する．$1$ 回の操作で袋の中のボールの個数は$1$減るので，$n-1$ 回の操作で袋の中のボールは $1$ 個になる．この最後の $1$ 個のボールに書かれた整数としてあり得るもののうち，最大値を $M (a)$ と表すことにしよう．

例えば，$a_1=1,\, a_2=2,\, a_3=3$ なら，$1,\,2$ を取り出し $2=\lceil (1+2)/2\rceil$ を袋に入れ，$2,\,3$ を取り出し $3=\lceil (2+3)/2\rceil$ を袋に入れると，残る整数は $3$ となる．同様に，はじめに $1,\,3$ を取り出すと最後に $2$ が残り，はじめに $2,\,3$ を取り出すと最後に $2$ が残る．よって，この場合は $M (a)=3$ となる．

(1)与えられた数列 $a$ に対して，$M (a)$ が得られるのはどのような取り出し方か．

(2) $F=(F_i)_i$ をフィボナッチ数列とする．つまり，$F$ は $F_1 = F_2 = 1$ かつ $F_{i+2} = F_{i+1} + F_{i}$ ($i \geqq 1$) という漸化式を満たす．$F$ を第 $n$ 項目までで打ち切った数列 $(F_i)_{1\leqq i \leqq n}$ を考え，$M_n = M ((F_i)_{1\leqq i \leqq n})$ と置く．このとき，非負整数 $n$ に対して，$M_{4n+1}$ を $\lceil \cdot \rceil$ を使わず表せ．

出題：北川宜稔 (九州大学マス・フォア・インダストリ研究所)