出題（2019年10月号掲載分）／応募締切（10月8日）／解答（2020年1月号掲載）
出題1
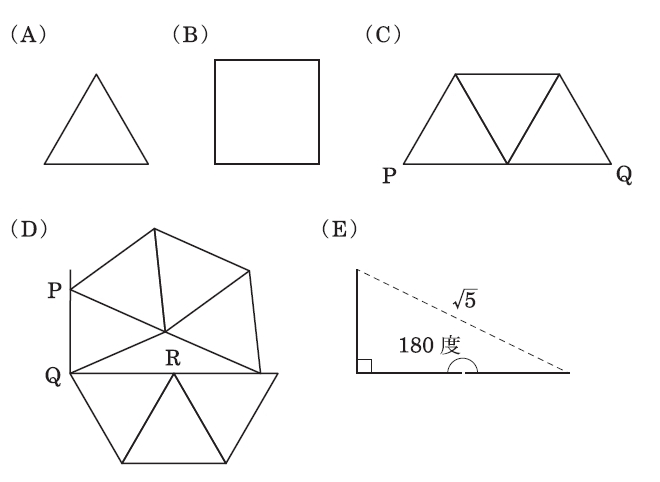
長さが 1 の線分だけを使って図形を描きます．そのとき，描かれた図形によって，線分どうしの相対的な位置関係が一意に決まる部分があるとき，その部分は「作図できた」と考えることにします．たとえば，図(A)では辺長 1 の正 3 角形の作図ができていますが，(B)では，各角が直角である保証はないので，これだけでは正方形の作図にはなりません．(C)では PQ の部分で長さ 2 の線分が作図できています．(D)の場合，一部の位置関係は確定していませんが，∠PQR の部分は確定しており，90 度の作図ができています．
(1)できるだけ少ない本数で(もし可能なら 8 本以内で) 90 度を作図してください．
(2)できるだけ少ない本数で(もし可能なら 8 本以内で) 20 度を作図してください．
(3) (2)で考えた 20 度というのは，いわゆる「コンパスと定規での作図」が不可能な角度です．そこで，その意味だと不可能ながら，本問での作図ルールなら 10 本以内の線分で作図可能な角度や長さの例((2)の答えから派生する自明なものを除きます)を見つけてください．ただし，そのままだと条件が厳しすぎるし，作図も煩雑になるので，「線分をまっすぐにつなげる」場合と「共通点をもつ線分どうしの角度を 90 度にする」場合に限っては，それらの部分の作図に必要な補助的な線分を省略してよいことにします．この場合，たとえば √5 は，(E)のとおり 3 本で作図できます．
(1)∼(3)のうちの一部だけの解答も歓迎します．
出題：岩沢宏和
出題2
正の実数の集合 {xtn} (n=0,±1,±2,⋯,t=0,1,2,⋯) において
xt+1n=min[xtn,xtn+1+xtn+2](n=0,±1,±2,⋯,t=0,1,2,⋯)が成り立つとします(min[a,b] は，a,b のうち大きくない方を表します)．さらに条件(1) (2)の一方が成り立つとき，ある整数 T が存在して，任意の n に対して T≦t ならば xtn=xTn となることを示してください．
(1) t=0 において，ある整数 N が存在し，任意の n に対して x0n+N=x0n が成り立つ．
(2) t=0 において，ある正の整数 N と，正の実数 α,β が存在し，N≦n ならば x0n=α, n≦−N ならば x0n=β が成り立つ．
出題：時弘哲治
応募規定［解答掲載2020年1月号］
郵送の場合
B5版の用紙をご使用のうえ，解答用紙 l 枚ごとにA：出題の番号(例：10月号出題1)，B：住所，氏名(ふりがなも明記，誌上での仮名を希望される方は，こちらに明記)，年齢，職業を記入して，下記宛先までお送りください．
〒170-8474 東京都豊島区南大塚3-12-4
日本評論社 数学セミナー〈エレガントな解答をもとむ〉係
メール送信の場合
B5版のサイズで，解答用紙 l 枚ごとにA：出題の番号(例：10月号出題1)，B：住所，氏名(ふりがなも明記，誌上での仮名を希望される方は，こちらに明記)，年齢，職業を記入して，下記フォームから PDF ファイルを送信して下さい．
解答記載に LaTeX ご利用の方は，テンプレートもご活用下さい．テンプレート利用は任意です．またテンプレートの漢字コードはUTF8です．ファイルが文字化けするときは適宜変換してお使いください．
投稿フォームが上手く動かないなどの場合は，susemi_elegant@nippyo.co.jp に直接お送り下さい．
注意事項
- 締切：2019年10月8日
- 二題に応募されるときは，郵送の場合は解答用紙を，メール送信の場合はファイルを，出題ごとにかえてください．
- 年齢を忘れずにお書きください．
- 解答用紙は両面の使用を不可とします．
- 解答用紙はご返却できません．
- 問題のご感想も歓迎します．
- 出題掲載号：数学セミナー2019年10月号
- 解答・講評は，本誌2020年1月号にてご確認ください．