出題（2019年1月号掲載分）／応募締切（1月8日）／解答（2019年4月号掲載）
出題1
n 個の実数 x1,⋯,xn からなる列 x=(x1,⋯,xn) に対して，先頭 i 個の部分和を si=x1+⋯+xi とし，
f(x)=max{min{s1,s2,⋯,sn},0}と定めます．つまり部分和がすべて正ならばその最小値を f(x) とし，そうでなければ f(x)=0 とします．また列 x の成分を j 個ずらして得られる列を
x(j)=(xj+1,xj+2,⋯,xn,x1,⋯,xj)とします．このとき，sn>0 ならば，
f(x(0))+f(x(1))+⋯+f(x(n−1))=snが成り立つことを示してください．
たとえば x=(e,π,−1) のとき，s3=e+π−1 です．一方，x(1)=(π,−1,e) の部分和は π,π−1,π−1+e で，f(x(1))=π−1です．同様の計算で
f(x(0))+f(x(1))+f(x(2))=e+(π−1)+0が得られ，これは s3 と一致します．
出題：徳重典英
出題2
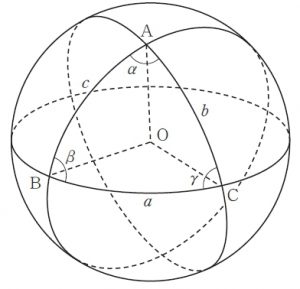
球面と平面の交わりは必ず円になります．このとき，交わりの円の直径が最大になるのは，平面が球面の中心を通るときです．この交わりの円を大円と呼びます．大円上の二点で定まる二つの弧のうち，長さの短い方を劣弧と呼びます．この大円が，平面上の幾何学における直線の役割を果たします．なぜなら，球面上の二つの点を結ぶ曲線のうち，長さを最小にするものが劣弧だからです．さて，図1にあるような点 O を中心とする半径 1 の球面を考えます．この球面上に三つの大円を描き，交点をそれぞれ点 A,B,C と名付けます．球面三角形 ABC とは劣弧 AB,BC,CAで囲まれた図形のうち面積の小さいもののことです．内角 ∠BAC とは弧 AB を含む平面と弧 AC を含む平面のなす角度のことです．また，半径を 1 としているので，弧 BC の長さは ∠BOC に一致します．ただし角度は弧度法で表すことにします．
図1 球面三角形
三辺の長さが a,b,c であり，対応する内角が α,β,γ である球面三角形に対して次の公式が成り立つことを示してください．
sinasinα=sinbsinβ=sincsinγ.ただし 3 頂点と球面の中心は同一平面上にはないと仮定します．
この公式は遥か昔から知られています．よく知られている証明は，球面三角法の余弦定理を先に示し，そこから式変形で導くものですが，ここではより直接的に幾何学的な考察から導いてみてください．
出題：深谷友宏
応募規定［解答掲載2019年4月号］
郵送の場合
B5版の用紙をご使用のうえ，解答用紙 l 枚ごとにA：問題の番号(例：1月号問1)，B：住所，氏名(ふりがなも明記，誌上での仮名を希望される方は，こちらに明記)，年齢，職業を記入して，下記宛先までお送りください．
〒170-8474 東京都豊島区南大塚3-12-4
日本評論社 数学セミナー〈エレガントな解答をもとむ〉係
メール送信の場合
B5版のサイズで，解答用紙 l 枚ごとにA：問題の番号(例：1月号問1)，B：住所，氏名(ふりがなも明記，誌上での仮名を希望される方は，こちらに明記)，年齢，職業を記入して，下記フォームから PDF ファイルを送信して下さい．
解答記載に LaTeX ご利用の方は，テンプレートもご活用下さい．テンプレート利用は任意です．またテンプレートの漢字コードはUTF8です．ファイルが文字化けするときは適宜変換してお使いください．
投稿フォームが上手く動かないなどの場合は，susemi_elegant@nippyo.co.jp に直接お送り下さい．
注意事項
- 締切：2019年1月8日
- 2 問に応募されるときは，郵送の場合は解答用紙を，メール送信の場合はファイルを，問題ごとにかえてください．
- 年齢を忘れずにお書きください．
- 解答用紙は両面の使用を不可とします．
- 解答用紙はご返却できません．
- 問題のご感想も歓迎します．
- 出題掲載号：数学セミナー2019年1月号
- 解答・講評は，本誌2019年4月号にてご確認ください．