Web日本評論 > 日評雑誌記事セレクション > 出題（2023年12月号掲載分）／応募締切（12月8日）／解答（2024年3月号掲載）

出題（2023年12月号掲載分）／応募締切（12月8日）／解答（2024年3月号掲載）

エレガントな解答をもとむ(数学セミナー)｜ 2023.11.13

『数学セミナー』のコーナー「エレガントな解答をもとむ」の出題を掲載します．奮ってご応募ください．解答・講評(3ヶ月後)は，本誌にてご確認ください．

(毎月10日頃の掲載予定)

$\def\t#1{\text{#1}}\def\dfrac#1#2{\displaystyle\frac{#1}{#2}}\def\a{\boldsymbol{a}}$

出題1

$N$ を正の整数，時刻を表す離散変数を $t=0,1,2,\cdots$ として，$0,\,1,\,2$ の 3 つの要素のみを持つ有限数列 $\a (t)=a_1 (t) a_2 (t)\cdots a_N (t)$ ($a_i (t) \in\{0,1,2\}$ ($i=1,2,\cdots,N$)) が，次の規則に従って時間発展するものとします．

(1) $t=0$ では，$\a (0)$ の要素は $0$ と $1$ のみである．

(2) $t \geqq 0$ において，$\a (t+1)$ は次の規則で $\a (t)$ から定まる．ただし，周期的な境界条件を考えており，$a_0 (t)=a_N (t)$, $a_{N+1}(t)=a_1 (t)$ とする．

$a_{i}(t)=0$ かつ $a_{i-1}(t)=1$ ならば，$a_i (t+1)=1$.
$a_{i}(t)=0$ かつ $a_{i-1}(t) \ne 1$ならば，$a_i (t+1)=0$.
$a_i (t)=1$ かつ $a_{i+1}(t)=0$ ならば，$a_i (t+1)=0$.
$a_i (t)=2$ かつ $a_{i+1}(t)=0$ ならば，$a_i (t+1)=1$.
$a_i (t)\ne 0$ かつ $a_{i+1}(t)\ne 0$ ならば，$a_i (t+1)=2$.

例えば，
\begin{align*}
\a (0)=&\,0\,1\,1\,0\,1\,1\,0\,0\,0\,1\,0\,1\,0\,1\,0\,1\,0\,1\,1\,1\\[5pt]
\a (1)=&\,1\,2\,0\,1\,2\,0\,1\,0\,0\,0\,1\,0\,1\,0\,1\,0\,1\,2\,2\,0\\[5pt]
\a (2)=&\,2\,1\,0\,2\,1\,0\,0\,1\,0\,0\,0\,1\,0\,1\,0\,1\,2\,2\,1\,0\\[5pt]
\a (3)=&\,2\,0\,1\,2\,0\,1\,0\,0\,1\,0\,0\,0\,1\,0\,1\,2\,2\,2\,0\,1
\end{align*}のようになります．

このとき，$\a (0)$ の要素に含まれる $1$ の数を $M$ ($1 \leqq M \leqq N$) とすると，$M \leqq \dfrac{N}{3}$ であれば，ある時刻以降は $\a (t)$ が $01$ 数列になること，すなわち，ある時刻 $T$ が存在して，$t \geqq T$ ならば必ず $\a (t)$ の要素は $0$ と $1$ だけになることを示してください．

出題：時弘哲治 (武蔵野大学工学部数理工学科)

出題2

いくつかの頂点と，いくつかの頂点同士を結ぶ線からなる構造をグラフという．このとき，頂点同士を結ぶ線を辺という．すべての頂点間に辺が 1 本ずつ存在するグラフを完全グラフという．グラフ上である頂点からスタートし，いくつかの異なる頂点を通ってもとの頂点に戻る経路を閉路という．完全グラフの各辺に 1 色ずつ色を割り当てて得られる辺着色グラフというものを考える．辺着色グラフの閉路において，隣接する 2 辺で同じ色のものが存在するとき，その閉路を良いと呼ぶことにする．

このとき，任意の閉路が良い閉路である辺着色グラフには，接続している辺がすべて同色の頂点が存在することを示せ．

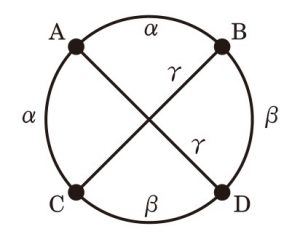
例えば，4 つの頂点 $\t{A},\,\t{B},\,\t{C},\,\t{D}$ があり，3 つの色 $\alpha,\,\beta,\,\gamma$ があるとする．このとき，頂点間を次の色で結んでできる辺着色グラフを考える．
\begin{align*}
\alpha:~\t{AB},\,\t{AC}\quad
\beta:~\t{BD},\,\t{CD},\quad
\gamma:~\t{AD},\,\t{BC}
\end{align*}

このとき，$\t{A}\to\t{B}\to\t{D}\to\t{C}\to\t{A}$ という経路は閉路になっており，頂点 $\t{A}$ にも頂点 $\t{D}$ にも同色の辺が接続しているので良い閉路である．一方で，$\t{C}\to\t{A}\to\t{D}\to\t{C}$ という経路は閉路ではあるが，各頂点に異なる色の辺が接続しているので良い閉路ではない．また，$\t{A}\to\t{B}\to\t{C}\to\t{D}\to\t{A}$ という経路も閉路ではあるが，良い閉路ではない．