Web日本評論 > お知らせ > 日評雑誌記事セレクション > 数学セミナー > 出題（2026年2月号掲載分）／応募締切（2月8日）／解答（2026年5月号掲載）

出題（2026年2月号掲載分）／応募締切（2月8日）／解答（2026年5月号掲載）

エレガントな解答をもとむ(数学セミナー)｜ 2026.01.09

『数学セミナー』のコーナー「エレガントな解答をもとむ」の出題を掲載します．奮ってご応募ください．解答・講評(3ヶ月後)は，本誌にてご確認ください．

(毎月10日頃の掲載予定)

$\def\t#1{\text{#1}}\def\dfrac#1#2{\displaystyle\frac{#1}{#2}}$

出題1

桁切り 2 乗和は自然数に対して決まる関数である．自然数 $x$ の 10 進数表現の各桁を $x_1, x_2, \cdots, x_n$ とすると，桁切り 2 乗和の関数 $f$ は
\begin{align*}
f (x)= x_1^2+x_2^2+\cdots +x_n^2
\end{align*}である．たとえば $f (314)=3^2+1^2+4^2=26$ になる．

任意の自然数 $x$ を初期値として桁切り 2 乗和を繰り返す数列を考える．つまり
\begin{align*}
x,\, f (x),\, f (f (x)),\, f (f (f (x))), \cdots
\end{align*}である．このとき，以下について答えよ．

(1)この数列が発散することはあるか．

(2)この数列が収束する場合，収束する値の候補を挙げよ．

(3)この数列が振動する場合，そのループの候補を挙げよ．

小谷善行 (東京農工大学名誉教授)

出題2

図 1 に 4 つ並んでいるような図形を根ね付き二分木といいます．いちばん上の頂点を根と呼び，そこから下に線が伸びます．各点は，下に 2 本の線を持つか，まったく持たないかのいずれかです．下に線を持たない点を葉はと呼びます．図 1 のように，葉には左から順に番号付けをします．根付き二分木 $T$ に対し，下に 2 本の線を持つ点の数 (分岐の数) を $C(T)$ とします．図 1 の場合，分岐の数は左から順に $3,\, 3,\, 2,\, 2$ です．

$C (T_1) = C (T_2)$ を満たす 2 つの木 $T_1,\, T_2$ の組を考えます．この組が既約でないとは，ある $i$ が存在して，両方の木で「$i$ 番目の葉と $i+1$ 番目の葉がそれぞれ同じ点から伸びている」ことをいいます．ここで「同じ点から伸びている」とは，ある 1 つの点から伸びている 2 本の線の先が $i$ 番目と $i+1$ 番目の葉であることを意味します．つまり，両方の木において，$i$ 番目の葉と$i+1$ 番目の葉がそれぞれひとつの分岐を構成しているという状況です．そのような $i$ が存在しないとき，この組は既約であるといいます．例えば図 1 の左側の組は， 2 の葉と 3 の葉がどちらの木においても共通の点 ♦，★ から伸びているので既約ではありません．右側の組は，1 つ目の木において 1 の葉と 2 の葉が分岐を構成していますが，もう 1 つの木の 1 の葉と 2 の葉は分岐を構成していません．2 の葉と 3 の葉は 1 つ目の木において分岐を構成していないので，この組は既約です．自然数 $n \geqq 2$ に対し，$N (n)$ を $C (T_1) = C (T_2) = n$ を満たす既約な二分木の組 $(T_1, T_2)$ の個数とします．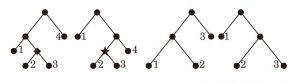

前置きが長くなりましたが，問題は以下の通りです．カタラン数 $c_n$ を$c_n = {}_{2n}\text{C}_n/ (n + 1)$ で定めます．任意の自然数 $n\geqq 2$ に対して，
\begin{align*}
2c_{n-1} \leqq N (n) \leqq c^2_n
\end{align*}が成り立つことを示してください．不等式評価の改良も歓迎します．

出題：児玉悠弥 (鹿児島大学大学院理工学研究科)