『数学がゲームを動かす!—ゲームデザインから人工知能まで』(著:三宅陽一郎,清木昌)
プロローグ 数学がゲームを動かす! (三宅・清木対談)
清木●数学は役に立たないって言われてますよね.
三宅●そうですよね.特に中高生のみなさんは,数学を勉強していて,何の役に立つんだってよく言ってますよね.

清木●でも,例えばゲームって数学がないとまったく動かない.
三宅●そうそう.ゲームは数学的な原理で動いているわけですから,とても役に立っています.
清木●ゲーム開発のプログラミングをしているときは,いかに数学的原理をコードに落としていくかってことを考えますね.
三宅●数学を知れば知るほどゲームのことが分かるんですよね.だから,この本では,ゲームを動かしている数学って具体的にこうなっている,ということをお伝えしたい.
清木●と,いきなり始まりましたが,まえがきでもあるこの序章では,本書の執筆者 2 人で雑談をしながら,この本の見所などをお伝えできればと思います.三宅さんはゲーム開発者として,もう長いですよね.何年ぐらいになりますか.
三宅●そうですね. 2004 年からなので,約 20 年ですね.
清木●私も三宅さんとほぼ同じぐらいの時期に就職しているので,お互い 20 年ぐらいゲームとかデジタルのエンタメを作り続けてきていますね.それで,三宅さん,数学って実際,ゲーム開発でどのような立ち位置でしょう.
三宅●ゲームの世界は数学を介して成立していますね.人工知能のこともそうですが,最後は数学的なものに帰結していって,それがプログラムになるみたいな流れですね.
清木●なるほど.なんというか,ゲーム開発における基盤みたいなものですね.
三宅●そうですね.作ったソフトウェアの根幹というか,骨格を与えてくれるみたいなイメージです.数学によってゲームが構造化され,特に動的な仕組みでは数学が本領を発揮します.ただここで言う「数学」は,とても幅広いものです.中学,高校で習う「数学」もたいへんよく使いますし,『数学セミナー』で扱われるような高等な「数学」もやはり使います.
清木●数値のバランスを扱う部分は,むしろ「算数」と言った方がよい領域もありますよね.なので,本書は直感的にわかりやすい部分が多いかと思います.数式がたくさん出てくるページもときどきありますが,説明を補助するための数式ですので,読むのがたいへんであれば,斜め読みしていただいても問題ありません.
三宅●「ゲームと数学がどのように接しているか」に着目してお読みいただければ,十分に楽しんでいただけると思います.
清木●さて,三宅さんはゲーム AI の第一人者ですけれども,普段ゲームがどう作られているのかをご存知ない方は,ゲームの AI がどうやって動いているのかもわからない,想像するのも難しいかもしれないですね.具体的にイメージできそうな例はありますか.
三宅●そうですね.例えばキャラクターが敵に囲まれていて,どの敵からやっつけようかという話があります.これを「ターゲッティング問題」と言います.弱い敵からやっつけるのか,強い敵を優先するのか,自分に向かってくる敵を先に倒すのか,弱い敵とは距離を取って,強い敵を早く倒した方がいいのか,などいろいろあります.そういう場合は評価値をつけて,数値で比較して,この敵を最初にやっつけるとか決めるわけです.すごく初歩的な話なんですけど,そこをどういうふうに評価関数を作ったらいいか,というのが数学だったりするんです.
清木●いま,「評価関数」という言葉が出てきましたが,「関数」って本来は数学の用語ですよね.ゲームを作るときにも,学校の数学で学んだ「関数」という概念を日々使っているということですね.
三宅●そうですね.例えば距離の 2 乗に反比例して評価値が減っていくのか,それとも距離の逆数の方がよいのか.グラフの形が違いますよね.どんな関数の形にしたら一番よいターゲッティングができるかなど,ゲーム開発の現場でよく考えます.「この場合はグラフは直線でよいのではないか」など,いろいろ議論しますね.
清木●例えば,10m 先にいる敵と 1m 先にいる敵,どちらにどのくらい注目したいのかというのは,ゲームやシチュエーションによって変わってくるわけですよね.
三宅●そうですね.本当に急激に注目度が下がるケースもあれば,そうでないケースもあります.そこを数式で表現しないといけないので,距離を入力としてどういう式を作ればいいのかを日常的に考えているということですね.身近な例としてはそんなところでしょうか.清木さんはゲーム開発における数学の利用については何かエピソードはありますか?
清木●本書について,糸井さん1)と雑談したときに教えてもらったエピソードが素敵だったのでぜひ紹介させてください.糸井さんが『糸井重里のバス釣り No.1』(任天堂,1997 年) を開発していたときの話なのですが,年の瀬のそろそろ完成という時期になっても,竿を振ってルアーを投げ入れるときの釣り糸の動きが硬くて,「このままじゃだめだよなー」と思っていらっしゃったようなのです.それが,年が明けたら,綺麗に糸がしなりながら飛んでいくようになっていた.どうやら,当時は開発会社のハル研究所でプロデューサーをしていたはずの岩田さん2)が正月に自ら実装されたらしく (笑)3).
三宅●さまざまな伝説が残る岩田さんらしいエピソードですね!
清木●糸が「スーパーファミコン」と思えない,実に色気のある挙動をしているんですよね.あの動きがあるだけで,グッと釣りをしている手応えが出る.そうした挙動を数値計算に落としこんでささっと作れるのは,数学の力だよね,という話を糸井さんとしていました.
三宅●ゲーム開発は,その場その場で求められることを何でもプログラミングしていく必要があるので,実装力が問われますね.その実装の構造を考え,ゲーム内の振る舞いを想像する力がまさに数学力ですね.
清木●私自身の話で言えば,新卒の時分にゲームプラットフォームのチームにいたので,いわゆる「SDK (Software Development Kit)」と呼ばれるゲーム開発者に使ってもらう開発キットを作っていたときの印象が強いですね.ゲームって最終的に見えているのはグラフィカルですが,そこに至るまでには,まずユーザーの入力を受け取り,それに応じてゲーム内の状態を更新して,最後にグラフィックスを描いて出力するようなシステムと言えます.
例えば,マイクを使って音声入力をするときに,入力データは波形データで入ってきますが,それをどう信号処理すれば,ゲームの入力として使えるものになるのかを考えることがあります.そういったときに周波数解析をしたいとなったら,フーリエ変換ができないといけません.また,ゲームはランダムな数がほしくなることが多いのですが,どのようにしてランダムに見える数を生成するのか,みたいなところでも数式が出てきます.コンピュータで扱うのは全部数字なので,数字に変換してそれを正しく処理していくという思考が必要になります.
三宅●どうしても数字とのやり取りは出てきますよね.ゲームではほとんど「データ」と「アルゴリズム」と言い換えることもできますが,原理的には数学で動いているようなものですからね.この本の題名にもある「数学がゲームを動かす」というのは的を射たフレーズだと思います.ゲーム全体も,音声の入出力も,ゲームキャラクターの AI も,いろいろなところで数学が駆動原理になっているというのはあります.コンピュータは数学によって,一段と高い機能を持つように質的変化しますね.
清木●特に 3D のゲームになると,ゲーム内に仮想の 3D 空間があって,そこに存在する多数のキャラクターをゲームの法則に従って $1/60$ 秒ごとに動かしていくという,リアルタイム 3D シミュレーションですからね.
三宅●高校数学で学ぶような空間幾何の世界そのものですよね.
清木●三角関数やベクトルを学んで社会で何に使うんだ,みたいな話がありますが,ここでいっぱい使います! 最近は,流体の動きや,光の反射のシミュレーションまでもリアルタイムでやりだしたりしています.ゲーム関連技術は本当に大変だなと.
三宅●そう聞くと大変そうだなと思う一方で,今は誰でもゲームが作れる時代にもなっているんですよね.こんなに数学をいっぱい使っているのに,それでも誰でも作れるというのは,繰り返し使われる処理が全部ライブラリやシステムの中に準備されていて,プログラムを直接書かなくても使えるようになっているからだと思います.ある意味,プログラムや数学をあまり考えなくても, 3D ゲームがある程度作れちゃうような環境が用意されているというのはすごいことですね.
清木●そうですよね.今はそのあたりが随分ブラックボックス化されてしまって,生々しい数学の部分が見えなくなってきている面はあります.
三宅●本当は数学がバリバリ動いていて,それを見るとすごくかっこいいはずなんですけど,全然見えなくなってきていて,しかも GPU などのハードウェアで高速に実行するための専門的な知識とも結びついているので,余計にわかりにくくなってきていますよね.
清木●正直,現代のゲーム開発において,全部の分野について深く理解している人というのは,もう超人レベルじゃないと難しいと思います.ただ,ゲーム開発をしているときに「ここは妥協できないな」と感じることがあるわけですが,それをやり遂げられる実装力は持っておく必要がありますよね.それが数学の知識だったりするわけですよ.
三宅●全体像がわかっていることが大切で,そこから先の,実際に困ったときに打開するための道を切り開く力になるのが数学の知識だと思います.
清木●数学の知識がなくても使える便利なライブラリがあるのは事実で,それを使えば多くのことができるようになっています.でも,ゲームというのは既存のルールから逸脱するところにも面白さがあるので,ライブラリが提供している機能以上のことをしたいというニーズは必ず出てきます.そういうときに,数学の力をどう使って実現するのかが問われるわけですよね.
三宅●そう,ゲームの可能性というのは,ライブラリの中に閉じ込められているわけではないのです.数学的な理解があってこそ,いろいろな工夫ができる.でも,ゲーム開発における数学の全体像がわかっていないと,ライブラリのパラメータを変えることくらいしかできなくなってしまう.そうなると,ゲームの可能性も限られてしまいます.だから数学の理解は,ゲームデザインの幅を広げるためにも重要です.
清木●本当にそうですよね.特に最近は VR (Virtual Reality; 仮想現実) やAR (Augmented Reality; 拡張現実) などの新しい表現が出てきて,現実空間との接点を持って相互作用するようになってきているので,また新しい数学の知識が必要とされる場面が増えてきていると思います.
三宅●これからのゲームに必要とされる数学の幅は,どんどん広がっていくでしょう.だからこそ,ゲームにおける数学の可能性をしっかり伝えていきたいですよね.この本では,そのためにいろんな事例を集めました.
清木●本書を通して,ゲーム開発における数学の重要性を感じていただければ嬉しいですね.
三宅●はい,ぜひ多くの方に読んでいただきたいです.特に,これからゲームがどういう可能性を持っているのかについて関心を持っている人には,数学の視点からゲームを見ることで,新しい発見があるのではないかなと思います.
清木●現在のゲームは,ある意味数学の積み重ねの上に成り立っているわけですから,数学的な視点を持つことで,ゲームをより深く理解できるようになるはずです.
三宅●ゲームの歴史を振り返ってみても, 1970 年代から今に至るまで,いろいろな数学が積み上げられてきました.確率論や線形代数,解析学など,本当にさまざまな数学がゲームを動かしてきました.
清木●まさに,ゲームは数学の塊みたいなものですよね.一方で,ゲームは新しいことをやって驚いてもらうことが価値のような側面もありますので,数学に解決してもらいたい新しい課題を常に抱えています.
三宅●ゲームは数学を応用する場であると同時に,新しい数学を生み出す原動力にもなっているんじゃないでしょうか.これからますますゲームと数学の関係は深くなっていくと思います.
清木●というところで,そろそろ各章の内容について触れていきましょうか.本書は 2 人で執筆しましたが,せっかくなので,互いの担当章で特に面白かった章について紹介するというのはどうでしょう.
三宅●そうですね.私がまず面白かったのは,Chapter 5「8-bit の動きの計算」ですね.コンピュータというのは最後にはビット列に落とし込まねばならず,そこが純粋な数学と違うところです.数学的原理がコンピュータの計算処理へと変換されていく様子を見るのは,なんだかとってもゾクゾクします.またゲームはいろいろな場面でバリエーションを作るために乱数を必要とします.Chapter 4「ゲームと乱数」では,限られた制約の中で,よい乱数を生成することを紹介しますが,これもまた数学的原理とコンピュータの計算処理の断面が見られて興味深いです.Chapter 8「対戦の面白さを支える数学」は数学の威力がもっとも直接的に現れるところで,オンライン上で対戦するユーザー同士を選択して結び付けているのは数学だ,というところが面白いです.
清木●私が面白いと思って書いたポイントが三宅さんにも伝わっていて嬉しいです.私が面白かったのは,まず,Chapter 6「デジタルゲームの空間と時間」です.ゲームと数学の一番基本的な関わり方を丁寧に説明してあり,数学が今日のゲームの中でどのように地に足をつけているのかを理解できる章ですよね.ゲームには,線形代数や 3D グラフィックス,人工知能など,単独の専門書が出ている技術領域がありますが,それらの全体像が摑めます.また,後半の怒濤のゲーム AI の章 (Chapter 10〜Chapter 14) も見所だと思っています.ここは三宅さんのご専門そのままでもあるのですが,ゲーム開発者以外に向けつつ,かといって一般向けでもなく,理系の素養を持っている方向けに書かれているというのが貴重ですね.
三宅●また,本書は単行本化するにあたって,ゲーム開発者のインタビューを追加収録しました.連載時にも掲載されていたゲームデザイナーの石川淳一さんのお話に加えて,セガに在籍されながら,ゲーム開発者向けの線形代数の教科書までも書いてしまった山中勇毅さん,1990 年代から「PlayStation 」,「PlayStation 2」など制約のあるハードウェア上でユニークなゲーム AI を設計してきた森川幸人さんからもお話を伺うことができました.
清木●山中さんが書かれた『セガ的 基礎線形代数講座』(日本評論社) は,ゲーム開発の視点から線形代数を整理し直した名著ですね.インタビューで 3名の開発者のそれぞれ違う立場から見た,ゲーム開発に必要な数学的なセンスのお話を伺うことができて,本書の内容がより立体的になったように思います.ゲーム開発における数学の関わりをさまざまな角度から俯瞰できる一冊になったのではないでしょうか.
三宅●読者の方々に,ゲーム開発の裏側にある数学の世界を感じていただけたら嬉しいです.そして,これからのゲームの可能性について,数学の視点から考えるきっかけになれば幸いです.
清木●ゲームが好きな方はもちろん,数学に興味がある方にも楽しんでいただける内容だと思います.ぜひ多くの方に手に取っていただきたいですね.
三宅●そうですね.この本を通して,ゲームと数学の深い関係を感じていただければと思います.
本書を楽しむガイド
おすすめの読み方
本書は,『数学セミナー』 2022 年 4 月号〜2023 年 3 月号までの連載「ゲームに宿る数学の力-デジタルゲームをめぐる数学」を改稿し,大幅に順番を入れ替え,新規原稿としていくつかのインタビューと対談を加えた上で,書籍化したものです.
本書の各章は独立していますので,興味の惹かれる章があれば,その章から読むことができます.
一方で,順番にお読みいただくと,ゲームの歴史を辿りりながら,数学との関わりがイメージできるような構成になっています.ゲームにおいて数字を扱うとはどういうことか,といった本質的な関わり方の話からスタートして,後半は,ゲーム AI とそれを支える数学の高度化の歴史もあり,歯ごたえのある内容も揃っています.
著者の 2 人の対談は冒頭と末尾にあります.また途中には,特に数学を顕著に使用されている 3 人のゲーム開発者へのインタビューも収録されています.解説章とインタビュー章を交互に読まれると,理解も深まるかと思います.
本書の執筆にあたり,青山学院大学理工学部の西山享教授に貴重なご助言をいただきました.心より感謝申し上げます.なお,本書に誤りがある場合は,すべて著者らの責任によるものです.
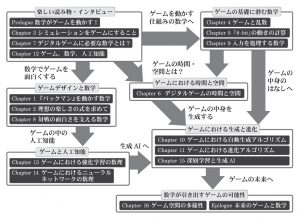
各章紹介
Chapter 1 は「パックマンの人工知能」についてです.デジタルゲームの名作である『パックマン』が,いかに数学的な設計になっているかを解説しています.この仕事は世界的に高く評価されており,デジタルゲームの人工知能 (AI) の出発点となりました.
Chapter 2 は「理想の楽しさの式を求めて」ということで,デジタルゲームがなかったアナログゲームの時代から,ゲームにおいてどのように戦闘が数値化されてきたのかを追っています.19 世紀のプロイセンの机上演習から,RPG に至るまでの旅です.
Chapter 3 は,シミュレーションゲームの第一人者である有限会社エレメンツの石川淳一さんへのインタビューを収録しています.アナログからデジタルへの移行期に,どのような工夫があったのかが語られていて,とても興味深い内容です.
Chapter 4 は「ゲームと乱数」ということで,ゲームにおけるランダム性の重要性と,その実現方法についてです. 1980 年代のアーケード筐体においてシンプルなハードウェア構成で疑似乱数を生成していた頃の話から,最新のゲームエンジンで採用されている乱数生成アルゴリズムまでを一望できます.
Chapter 5 は「「8-bit」の動きの計算」.ここでは,初期のゲーム機の制約の中で,いかに数学的なテクニックを駆使して,気持ちのよいキャラクターの動きを表現していたかを解説しています.簡単な掛け算ですら重い処理だった時代は,今となっては昔話ですが,こうした強い制約の中で磨かれた技術や考え方には,ある種の本質が切り取られているのではと感じています.
Chapter 6 は「デジタルゲームの空間と時間」です.ゲームならではの空間と時間の扱い方について,数学的な視点から考察しています.ユーザーにとってゲームとはまさに時間と空間を与えてくれるものですが,ゲーム内の AI にとっても同様です.AI が時間と空間をどう認識し,どう行動を創造していくか,について解説しています.
Chapter 7 は「デジタルゲームに必要な数学とは?」ということで,ゲーム開発の最前線で活躍されている株式会社セガ開発技術部の山中勇毅さんへのインタビューになります.長年,実務の現場を見てきた立場から,ゲーム開発における数学の重要性について語っていただきました.
Chapter 8 は「対戦の面白さを支える数学」,Chapter 9 は「入力を処理する数学」と,ゲームと数学という切り口の中では少し変わった分野を扱います.対戦の章では,フェアな対戦を支えている,プレイヤーの実力を数値化するアルゴリズムを紹介しています.理論的な背景も含めたレーティングアルゴリズムの解説は,日本語では珍しいかもしれません.入力処理の章では,ゲーム関連技術の幅の広さの例として,カルマンフィルタやパーティクルフィルタを題材に取り上げていますが,こちらは専門の良書がたくさんあるので,こうした世界もあるという入口としていただければ幸いです.
Chapter 10 以降は,ゲーム AI に関する,より今日的な数学の話題が並びます.将棋の世界から最新のゲーム AI まで,数学の力でゲームがどのように進化しているのかがわかる内容です.
Chapter 10 は「ゲームにおける自動生成アルゴリズム」.木の形から地形,果ては星系まで,さまざまなアセットを生み出す数学的自動生成アルゴリズムについて扱います. Chapter 11 は「ゲームにおける進化アルゴリズム」です.生物の進化にヒントを得て,ゲームのさまざまなものが進化を重ねていく,遺伝的アルゴリズムについて解説します.キャラクターの動きから,ゲームのルールそのものまで,多様な応用例をご紹介します.
Chapter 12 には,AI 技術を活用したさまざまなゲームを開発されてきたモリカトロン株式会社の森川幸人さんへのインタビューもあります.企画書に数式が直接書かれている森川さんのゲームデザイン手法をぜひ参考にしてください.
Chapter 13 は「ゲームにおける強化学習の数理」,Chapter 14 は「ゲームにおけるニューラルネットワークの数理」と,ホットトピックである機械学習系の技術について,ゲームという応用においてどう活用されているかを分かりやすくご紹介します.特に囲碁のプロ棋士に勝利した『AlphaGo』(Deep Mind 社,2015 年) でも使われている強化学習の手法 (DQN) は応用の幅が広く,格闘ゲームへの応用などについて解説しています.
Chapter 15 は「深層学習と生成 AI」.これから世の中を変えていく技術として言及を避けることができない,ディープニューラルネットワーク (DNN) について,数値計算という切り口でご紹介しています.
Epilogue は「ゲームの未来と数学」ということで,これから数学がゲームにどのような影響を与えていくのかを予想しつつ,本書のまとめとしています.
脚注
| 1. | ↑ | 株式会社ほぼ日社長の糸井重里氏.ゲーム分野では『MOTHER』シリーズの開発者としても知られる. |
| 2. | ↑ | のちに,任天堂株式会社の社長を務められた岩田聡氏. |
| 3. | ↑ | 当時,開発に参加していたハル研究所元社長の三津原敏氏にこのエピソードを伺ったところ,糸の挙動の実装者は把握できていなかったものの,たしかに岩田さんが糸のしなり具合を気にされていたこと,いつの間にか,とても動きが良くなっていたこと,そして,気になって実装を確認してみたところ,アセンブリ言語で書かれた難解なコードが並んでいた,とのことであった.なお,本作は 1997 年 2 月 21 日発売であり,新年すぐに納品であったと思われる |